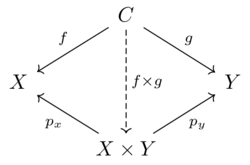
This is another object in \(\mathcal{C}\) with morphisms \(X \xleftarrow{p_x}X\times Y\xrightarrow{p_y}Y\)
This should satisfy the property that there exists a unique morphism making the following diagram commute for any other object C and morphisms \(X \xleftarrow{f}C\xrightarrow{g}Y\)